Here, we will derive formulas for European style Asian call and put options when we are taking geometric average of the underlying’s price. We will put expectation and variance of the geometric average into Black’s formula (generalized version), and will simplify it to obtain option formulas.

The geometric average is defined by

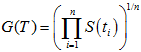
And, the continuously sampled geometric average is defined to be

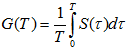
In both continuous and discrete cases, the variable G(T) lognormally distributed. Hence, in continuous case, we can write

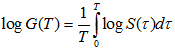
Or, equivalently

So, the resultant is normal distribution, and Kemna and Vorst showed its expectation and variance and derived the European style average call and put option formulas. The expectation and variance is given by

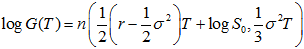
Where n(a,b) represents a normal distribution with mean a and variance b. Here,

and

Now, we need to put these two values in Black’s formula (generalized version)

First take

Where

Now consider

Using

We have

Setting

We have

For simplicity, we set

So now

Hence,

By putting all these values in Black’s formula, and by setting

we obtain the formula for geometric Asian call and put option formulas as follows