Stochastic Process → Definition → Poisson Process → Definition
Definition
For fixed rate λ>0, a counting process is called a Poisson process {N(t), t∈[0,∞)} if the following three conditions are hold:
1. N(0) = 0
2. N(t) has independent occurrences
3. The occurrences in the time interval t>0 has Poisson distribution, i.e.

It can be written in n or x. In solving the problems on probability of a Poisson processes, we use the following shape of the formula for convenience
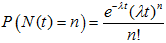
In all the three shapes of the formula, we have,
t = time interval
λ = rate
n or x = number of occurrences
SOME EXPLANATION
1. N(0) = 0 means the number of occurrences are zero when the counting is started. For example, if we start counting the customers in a shop that follows Poisson process at 9:00 then N(9) = 0
2. N(t) = 0 has independent occurrences means the arrivals are independent. For example, the arrivals of customers in a shop do not depend on each other. They can enter the shop when they want.
3. The occurrences or arrivals follows the Poisson distribution.
NOTE: Mean = λt, so when only mean is given and not the time and rate separately, then take λt = mean.