Mathematics → Subject Test → Eigenvalues and Eigenvectors

Suppose A is a square matrix. The relation for finding Eigenvalue λ corresponds to the Eigenvector X is

AX = λX

Practice Problems
Example 1. Find Eigenvalue corresponds to the Eigenvector

for matrix

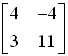
Solution
As we know that AX = λX
So,

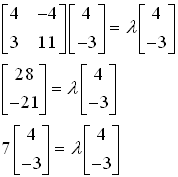
Hence, λ = 7 Answer

How to find Eigenvalues of a matrix?
To find eigenvalues of a given matrix, we have to use the relation
det ( λI – A ) = 0

Example 2. Find all the eigenvalues of the matrix

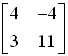
Solution
As we know that det ( λI – A ) = 0
Now,

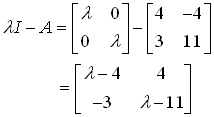
Now find determinant of λI – A
det ( λI – A ) = ( λ–4 ) ( λ–11 ) – ( –3 ) ( 4 )
= λ² – λ11 – λ4 + 44 + 12
= λ² – λ15 + 56

Now set this equal to zero to obtain det ( λI – A ) = 0 and solve for the eigenvalues.
λ² – 15λ + 56 = 0
λ² – 8λ – 7λ + 56 = 0
λ( λ – 8 ) – 7 ( λ – 8 ) = 0
( λ – 7 ) ( λ – 8 ) = 0 ⇒ λ₁ = 7, and λ₂ = 8
So we get two eigenvalues. Answer