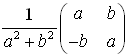Mathematics → Subject Test → Inverse of a Matrix

How to find Inverse of a Matrix?

To find inverse of a matrix, first we must check whether the matrix is singular or invertible. Here we find inverse of a 2 x 2 matrix.

Singular OR Invertible Matrix
Consider a Matrix

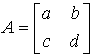
If ad – bc = 0, then the matrix is said to be a Singular Matrix.
If ad – bc ≠ 0, then the matrix is said to be an Invertible Matrix.
The inverse of a matrix only exists if the matrix is invertible.

Theorem
Consider a matrix

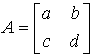
If the matrix is invertible, then its inverse is,

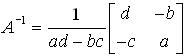
Practice Problems
Example 1. Show that A is an invertible matrix and find inverse, when

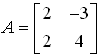
Solution
First check whether the matrix is invertible or not
ad – bc = (2)(4) – (2)(–3) = 8 + 6 = 14 ≠ 0
So, the matrix is invertible, now find its inverse,

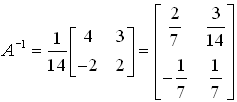
Example 2. Find inverse of the matrix

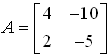
Solution
First check whether the matrix is invertible or not
ad – bc = (4)(–5) – (2)(–10) = –20 + 20 = 0
So, the matrix is singular. And its inverse does not exists.

Consider question No.3 of GRE Mathematics (GR9768)

Example 3. If

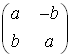
is invertible under matrix multiplication, then its inverse is?

Solution
Recall the definition (theorem) of inverse of a matrix
If

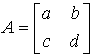
is invertible, then

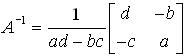
So the inverse of the given matrix is,