Mathematics → Subject Test → Integration by Parts

First of all, why Integration by Parts?
As we know that

But what’s the integration of

So, we use integration by parts technique for the integration of product of functions ( x and cosx in product form ).

Formula for Integration by Parts
Suppose two functions u and v are in product form, then formula for finding their integration is

We can also remember the short formula for Integration by Parts which is usually without dx

Practice Problems
Example 1. Evaluate
Solution
Here,
u = x ⇒ u’ = 1
v = cosx ⇒

Now using Integration by Parts formula
 We have,
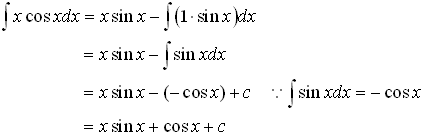 Answer

Example 2. Evaluate
Solution
Here,
u = 2x² ⇒ u’ = 4x
v = sinx ⇒
 Now using Integration by Parts formula
We have,
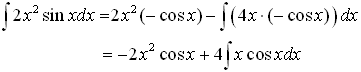The later is again product of functions, and we have to use Integration by parts again. In the example above we have already found that, so using result from the above, we have
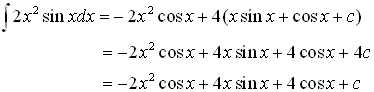Answer
NOTE: 4c and c both are constants, so ignore 4.