Mathematics → Subject Test → Cayley-Hamilton Theorem

Definition
Cayley-Hamilton Theorem states that every square matrix satisfies its own characteristic equation.

That is, if p (λ) = det ( A – λI ) is the characteristic polynomial of the matrix A, then according to Cayley-Hamilton Theorem p ( A ) = 0

For example,
If p (λ ) = det ( A – λI ) = λ² – λ15 + 56 is the characteristic polynomial, then by Cayley-Hamilton Theorem A² – 15 A + 56 I = 0
The following examples will make the matter more clear.

Practice Problems
Example 1. If
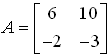then show that A³ = 7 A – 6 I
Solution

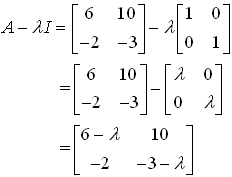
the characteristic polynomial of A is

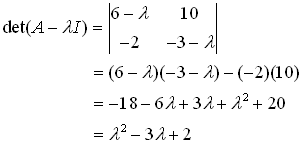
Now, by Cayley-Hamilton Theorem
A² – 3 A + 2 I = 0 ——> (1)
From (1): A² = 3A – 2 I
multiply A on both sides of above equation
A³ = 3A² – 2A ——–>(2)
Put A² = 3A – 2 I in equation (2)
(2)⇒ A³ = 3 ( 3A – 2 I ) – 2A
A³ = 9A – 6 I – 2A
A³ = 7A – 6 I Answer

Example 2. If

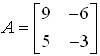
then show that A⁵ = 981 A – 540 I

Solution
The characteristic polynomial of A is

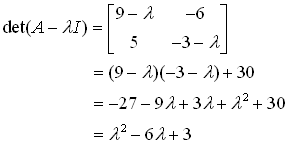
Now, by Cayley-Hamilton Theorem
A² – 6 A + 3 I = 0 ——> (1)
From (1): A² = 6 A – 3 I
multiply A on both sides of above equation
A³ = 6 A² – 3 A ——–>(2)
Put A² = 6 A – 3 I in equation (2)
(2)⇒ A³ = 6 ( 6 A – 3 I ) – 3 A
A³ = 36 A – 18 I – 3 A
A³ =33 A – 18 I
multiply A² on both sides of above equation
A⁵ = 33 A³ – 18 A² ——–>(3)
Put A² = 6 A – 3 I and A³ =33 A – 18 I in equation (3)
(3)⇒ A⁵ = 33 ( 33 A – 18 I ) – 18 ( 6 A – 3 I )
A⁵ = 1089 A – 594 I – 108 A + 54 I
A⁵ = 981 A – 540 I Answer